Data structures: 2-3 tree

The main problem of binary search trees – necessity to keep them balanced. When this requrement is not met – perfomance of operations degrades significantly. Imagine a simple binary tree…you start inserting the data preserving its order. In that case tree is basically turned into linked list with all the ensuing consequences: search in O(N), so all advantaged of binary tree are completely wasted.

There are many special types of trees that perform insert/remove operation in intelligent way ensuring that result tree is small but branchy :). This trees are called self-balanced, most well-known of them are AVL trees, Red-black trees, 2-3 trees. This post is dedicated to the latter ones.

Non-leaf nodes in 2-3 tree can be either 2 node of 3 node.

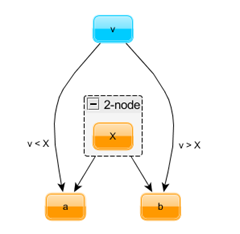
2 node

Node invariants:

• value of every node in subtree a is lesser than X
• value of every node in subtree b is greated than X
• length of path from 2-node to all descendant leaf node is the same

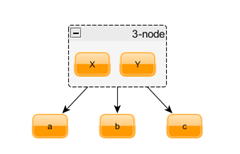
3-node

Node invariants:

• value of every node in subtree a is lesser than X
• value of every node in subtree b is greater than X and lesser than Y
• value of every node in subtree c is greater than Y
• length of path from 3-node to all descendant leaf node is the same

Invariants in italic guarantee that all elements in tree are ordered. Bold invariants keep tree balanced and ensure that height of tree cannot be greater than log2(N + 1).

During all operations with tree it is essential to maintain all invariants. Let's deconstruct and analyze insert operation:

1. First of all we need to find acceptable insert location. For this we'll traverse top-to-bottom, compare new value with values in data slots and choose subtree relying on result of comparison.

   

   

   It doesn't matter what subtree is used for equal nodes, the main thing is that selection strategy must be used everywhere.

2. When descent reaches the leaf node we cannot simply create new 2-node with two empty subtrees, this will violate the invariant because height of new subtree shall differ from height of remaining tree. Instead we will notify parent and send him triple with new value and its left and right subtrees. As a response parent can consume arguments and transform itself, or it can it turn push notification up to its parent. This will continue until top level tree node consume notification (tree become wider) or notification is propagated to the outside - in that case we will create new 2-node with value and subtrees taken from notification (tree height increased).

F# tree type declaration

type TwoThree<'T> = 
    | Leaf
    | Two of 'T * TwoThree<'T> * TwoThree<'T>
    | Three of 'T * 'T * TwoThree<'T> * TwoThree<'T> * TwoThree<'T>

Push notification arguments:

type PushedValue<'T> = {Value: 'T ; Left : TwoThree<'T> ; Right : TwoThree<'T>} 

Insert routine uses values of Choice union for deliverig insertion results to parent. Choice1Of2 means that value was successfully consumed on the bottom levels and result - new subtree that should be included instead of old one. Choice2Of2 carries push value notification.

let insert v t = 
    let rec add v = function
        | Leaf -> Choice2Of2 <| {Value = v; Left = Leaf; Right = Leaf}
        // special cases to handle terminal nodes
        | Two(x, Leaf, Leaf) when x < v-> Choice1Of2 <| Three(x, v, Leaf, Leaf, Leaf) 
        | Two(x, Leaf, Leaf) -> Choice1Of2 <| Three(v, x, Leaf, Leaf, Leaf)
        | Three(x, y, Leaf, Leaf, Leaf) when v < x -> Choice2Of2 <| {Value =  x; Left = Two(v, Leaf, Leaf); Right = Two(y, Leaf, Leaf)}
        | Three(x, y, Leaf, Leaf, Leaf) when v < y -> Choice2Of2 <| {Value =  v; Left = Two(x, Leaf, Leaf); Right = Two(y, Leaf, Leaf)}
        | Three(x, y, Leaf, Leaf, Leaf) when v > y -> Choice2Of2 <| {Value =  y; Left = Two(x, Leaf, Leaf); Right = Two(v, Leaf, Leaf)}
        | Two(x, l, r) ->
            if v < x then
                match add v l with
                | (Choice1Of2 newL) -> 
                    Choice1Of2(Two(x, newL, r)) // value was consumed on the inner levels
                | (Choice2Of2 ({Value = kv; Left = kl; Right = kr})) ->                 
                    Choice1Of2(Three(kv, x, kl, kr, r)) // consume
            else 
                match add v r with
                | (Choice1Of2 newR) -> 
                    Choice1Of2(Two(x, l, newR)) // value was consumed on the inner levels
                | (Choice2Of2 ({Value = kv; Left = kl; Right = kr})) ->                 
                    Choice1Of2 (Three(x, kv, l, kl, kr)) // consume
        | Three(x, y, l, m, r) ->
            if v < x then
                match add v l with
                | (Choice1Of2 newL) -> 
                    Choice1Of2(Three(x, y, newL, m, r)) // value was consumed on the inner levels
                | (Choice2Of2 ({Value = kv; Left = kl; Right = kr})) ->                 
                    Choice2Of2 ({Value = x; Left = Two(kv, kl, kr); Right = Two(y, m, r)}) // send push notification
            else if v < y then
                match add v m with
                | (Choice1Of2 newM) -> 
                    Choice1Of2(Three(x, y, l, newM, r)) // value was consumed on the inner levels
                | (Choice2Of2 ({Value = kv; Left = kl; Right = kr})) ->                 
                    Choice2Of2 ( {Value = kv; Left = Two(x, l, kl); Right = Two(y, kr, r)}) // send push notification
            else 
                match add v r with
                | (Choice1Of2 newR) -> 
                    Choice1Of2(Three(x, y, l, m, newR)) // value was consumed on the inner levels
                | (Choice2Of2 ({Value = kv; Left = kl; Right = kr})) ->                 
                    Choice2Of2 ( {Value = y; Left = Two(x, l, m); Right = Two(kv, kl, kr)}) // send push notification

    match add v t with
    | Choice1Of2 v -> v // top level tree consumed all changes
    | Choice2Of2 {Value = v; Left = l; Right = r} -> Two(v, l, r) // push notification appear on the top level - increase tree height

Inserting values from 1 to 10

In my next post the talk will turn to finger tree, general purpose data structure based on 2-3 tree. Stay tuned!

Update: C# version