Data structures: Finger Tree (Part 1.5)

Last time we stopped on “immutable deque” stage. Today we will explore a few additions that can endow deque with super (hmm..human/deque?) powers.

Random access

One of the most popular and claimed abilities of data structures nowadays is random access. The BCL leader in this category is undoubtedly List (O(1)), in opposite LinkedList has the worst results - O(N). What should we change in structure of the tree to make it support random access? Surprisingy - a little. Let's describe this on the simplified sample with binary tree containing data in the leaf nodes.

To extend tree with efficient random access capabilities we will annotate all nodes with its size. Size of leaf node is always 1 and size of non-leaf = sum of sizes of its immediate children. The change we made is seems to be minor but this is the one that adds very important features:

• Annotation on the top level returns total number of items in tree
• Accessing element by index boils down to recursive descent plus optional index fixup.

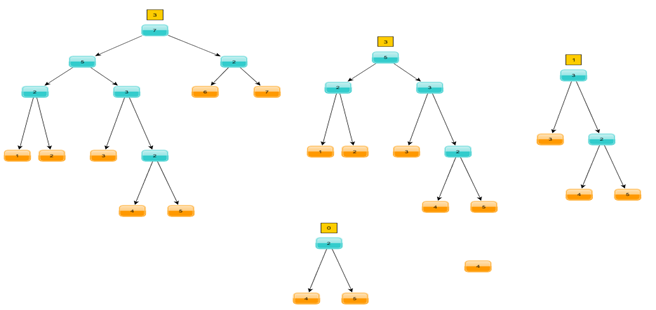
For example we want to take element with index 3 (starting with 0) from the tree gived in sample above .First of all we need to ensure that required index belongs to tree. Index(3) is lesser than size of root node (7) so it is definitely in tree.

Step 1: Node – root (7), index 3 and we need to select one of subnodes. Size of left subnode 5, so it contains index range [0..4]. Required index fall within this range then we move to the left with index unchanged.

Step 2: Node (5), index – 3. Size of left subnode 2 and now it is lesser than required index -we select right subnode. Index is fixed  according to the rule:new-index = old-index – size-of-left-subnode 

Step 3: Node (3), index 1  and it is once again greated than size of left subtree. We know what to do: move to the right, fix index

Step 4: Node (2), index 0, it is lesser then size of left subnode (1) – move to the left without touching index.

Step 5: We’ve reached the leaf – success!!!

Picture below illustrates process of descending step by step. Number in yellow brick – index on current stage.

type Tree<'T> = 
    | Leaf of 'T 
    | Node of int * Tree<'T> * Tree<'T>

let size = function
    | Leaf _ -> 1
    | Node (s, _, _) -> s

let leaf v = Leaf v
let node l r = Node(size l + size r, l, r)

let rec find i = function
    | Leaf v when i = 0 -> v
    | Node(_, l, r) ->
        let ls = size l
        if i < ls then find i l
        else find (i - ls) r
    | _ -> failwith "incorrect index"

let tree = node (node (node (leaf 1) (leaf 2))  (node (leaf 3) (node (leaf 4) (leaf 5)))) (node (leaf 6) (leaf 7))
let res = find 3 tree // 4

Note: we’ve used custom function node instead of constructor Node to automatically calculate size of non-leaf nodes. Such functions that do something besides simple constructor calls are usually named smart constructors

If the tree is balanced (and finger tree is always balanced) then such implementation of random access will be O(log(N)).

Max-priority queue

Let’s consider another problem, we need data structure that stores items with associated values (priorities) and provides efficient access to element with maximum priority.

To extend tree with such capabilities we will annotate all nodes (I know that it sounds familiar). In this case value of annotation in every leaf node shall be value of priority itself. As for the non-leafs - they shall be annotated with value of maximum priority it contains. The concept of solution remains the same: we travel from top to bottom of the tree, on every non-leaf level we select one of subnodes that contains maximum priority. When leaf node is reached – success.

type Tree<'T> = 
    | Leaf of int * 'T 
    | Node of int * Tree<'T> * Tree<'T>

let priority = function
    | Leaf (p, _) -> p
    | Node (s, _, _) -> s

let leaf v = Leaf v
let node l r = Node(max (priority l) (priority r), l, r)

let rec find = function
    | Leaf(_, v) -> v
    | Node(_, l, r) ->
        let lp = priority l
        let rp = priority r
        if lp > rp then find l
        else find r

let tree = node (node (node (leaf (5, 2)) (leaf (3,3)))  (node (leaf (10, 5)) (node (leaf (11, 6)) (leaf (2, 9))))) (node (leaf (4, 10)) (leaf (7, 12))) // 6

Efficiency of this version also depends on the fact whether tree is balanced and in the best case it is O(log(N)).

As you may notice the structure of the tree remains almost the same (in fact we can use it in random access sample too and just assign constant size to Leaf in leaf smart constructor). The only thing that changed is annotation. To unify both implementation we need associative binary function for combining values (ie (+) or max) and some kind of zero value that can be combined with any other value (V) from the domain and return V unchanged. Google prompts the answer - this is monoid. For random access monoid components are mapped on (+) as Combine and 0 as Zero. For max-priority queue Zero is int.MinValue and Combine - max. Code below illustrates possible implementation of unified approach in F#

type IMeasured<'V> = 
    abstract Value : 'V

let measure (v : #IMeasured<_>) = v.Value

type IMonoid<'V> = 
    abstract Zero : 'V
    abstract Plus : 'V -> 'V -> 'V

type Singleton<'T when 'T : (new : unit -> 'T)> private () = 
    static let instance = new 'T()
    static member Instance = instance

type Tree<'T, 'M, 'V when 'M :> IMonoid<'V> and 'M : (new : unit -> 'M) and 'T :> IMeasured<'V>> = 
    | Leaf of 'T 
    | Node of 'V * Tree<'T, 'M, 'V> * Tree<'T, 'M, 'V>
    interface IMeasured<'V> with
        member x.Value = 
            let monoid = Singleton<'M>.Instance
            match x with
            | Leaf v -> v.Value
            | Node(v, _, _) -> v

let node<'T, 'V, 'M when 'M :> IMonoid<'V> and 'M : (new : unit -> 'M) and 'T :> IMeasured<'V>> (l : Tree<'T, 'M, 'V>) (r : Tree<'T, 'M, 'V>) = 
    let monoid = Singleton<'M>.Instance
    Node(monoid.Plus (measure l) (measure r), l, r)

[<RequireQualifiedAccess>]
module RandomAccess = 
    type Monoid() = 
        interface IMonoid<int> with
            member this.Zero = 0
            member this.Plus a b = a + b
    type Element<'T> = 
        { Value : 'T}
        interface IMeasured<int> with
            member this.Value = 1
    
    let createLeaf v = Tree<Element<_>, Monoid, int>.Leaf ({Value = v})
    let createNode l r= node<Element<_>, int, Monoid> l r
    let rec nth i = function
        | Leaf {Value = v} when i = 0 -> v
        | Node(_, l, r) ->
            let ls = measure l
            if i < ls then nth i l
            else nth (i - ls) r
        | _ -> failwith "invalid index"

[<RequireQualifiedAccess>]
module Priority = 
    type Monoid() = 
        interface IMonoid<int> with
            member this.Zero = System.Int32.MinValue
            member this.Plus a b = max a b
    type Element<'V> = 
        { Prio : int
          Value : 'V }
          interface IMeasured<int> with
            member this.Value = this.Prio

    let createLeaf = Tree<_, Monoid, int>.Leaf
    let createNode l r= node<Element<_>, int, Monoid> l r
    let rec find = function
        | Leaf ({Value = v}) -> v
        | Node(_, l, r) ->
            let ls = measure l
            let rs = measure r
            if ls < rs then find r
            else find l

Next time we will link together implementation of finger trees and power-ups from todays post.